Центральная предельная теорема python

Введение в анализ данных
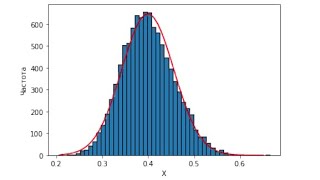
Edit and run. Вывод: можно заметить, что с ростом числа n гистограмма становится все более гладкой и все более похожей на нормальное. ЦПТ в данном случае работает. In [1]:.


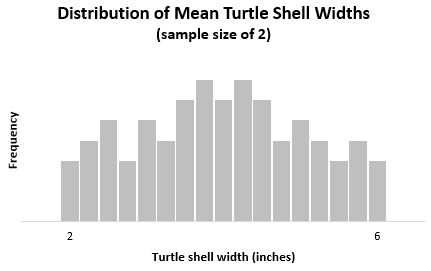
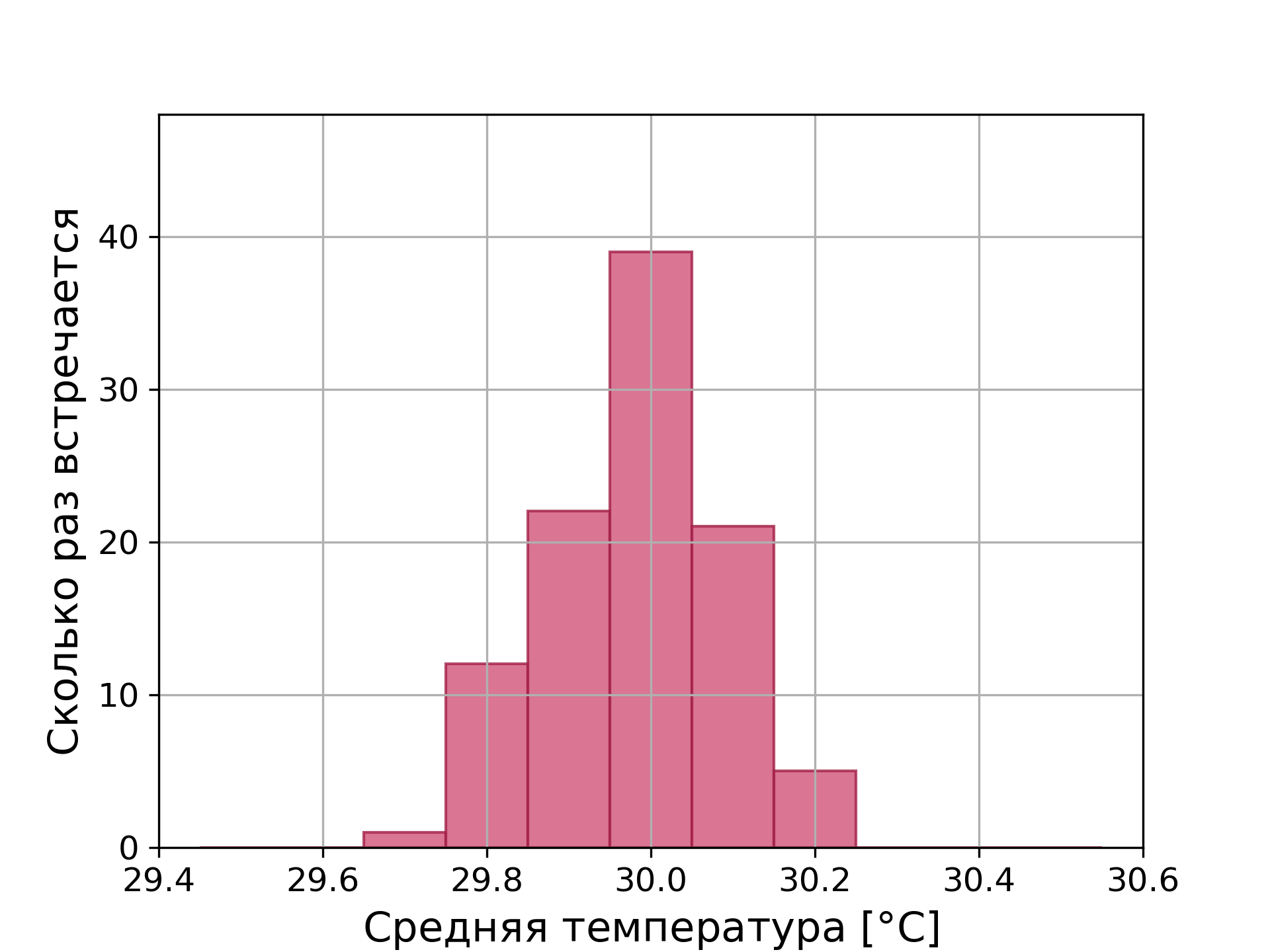





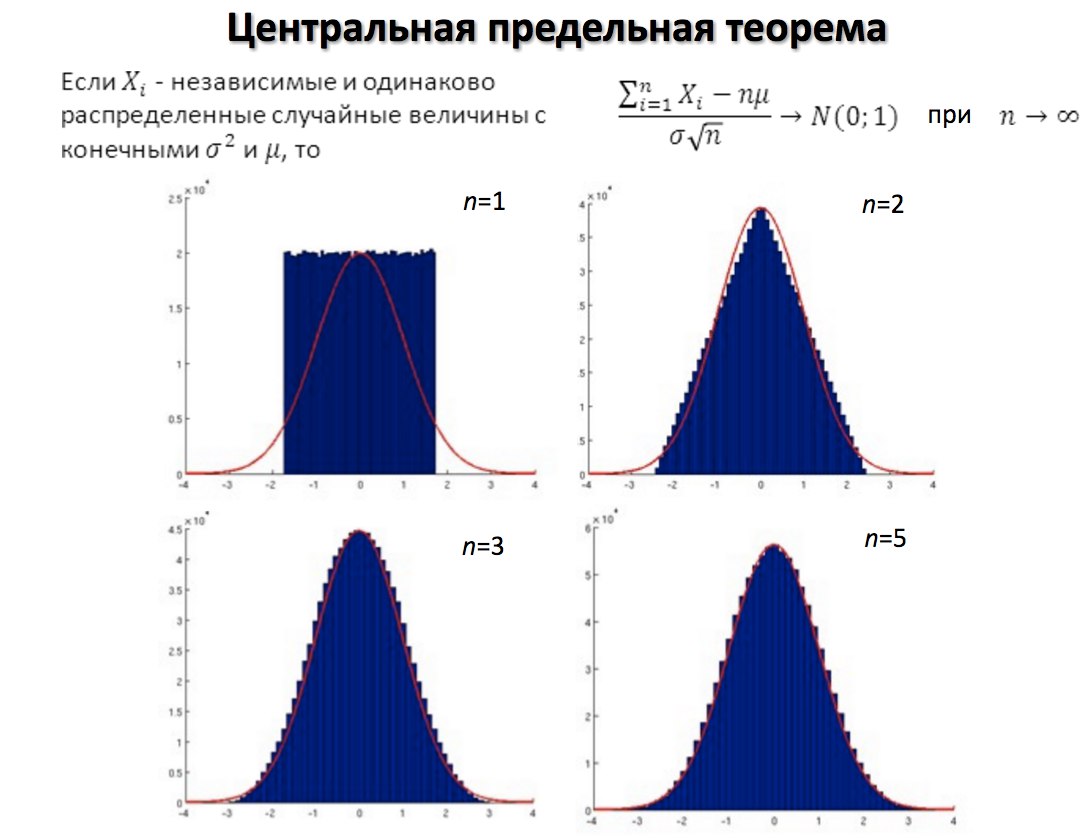
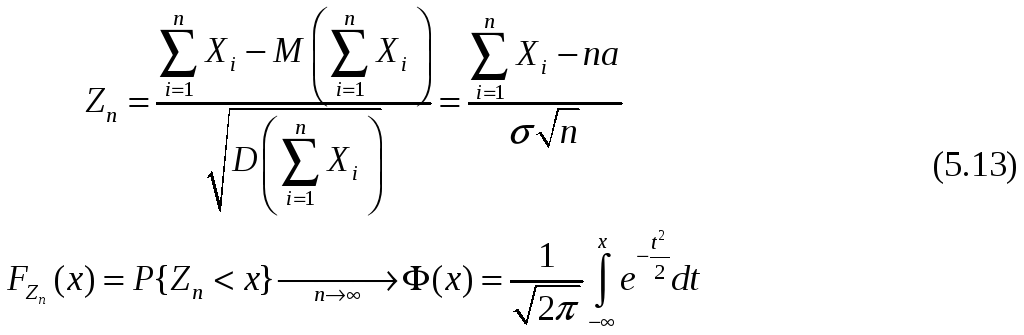
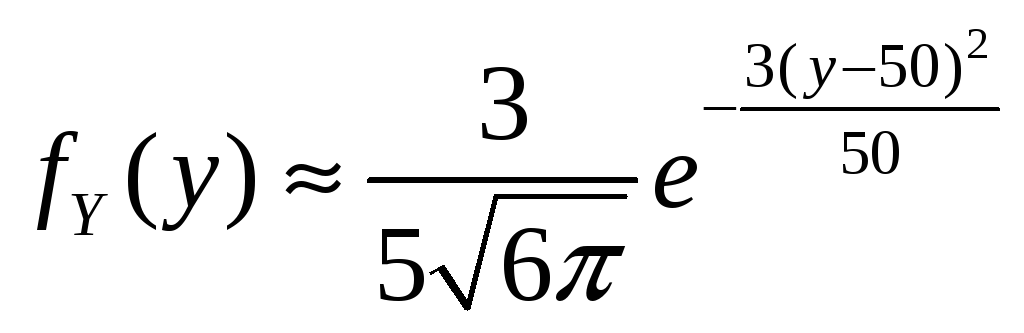
Интуитивно кажется, что да, но неплохо бы собрать данные и проверить это предположение. В этом параграфе мы расскажем, какие инструменты существуют для оценки данных, что есть «много», «мало», «нормально» и почему всё относительно. Как вы уже поняли, статистика любит точность и вопросы. Поэтому вместо «что есть мало? Эти три вопроса сводятся к одному понятию — распределению наблюдений относительно друг друга.





Фундаментальным понятием теории вероятностей, на котором базируются многие прикладные решения является Центральная предельная теорема. Нормальное распределение имеет следующую колоколообразную форму и показывает плотность вероятности значений случайной величины, то есть в нашем случае основная доля сосредоточена вокруг 6, а затем вероятности остальных интервалов убывают по мере удаления от него:. Проверим истинность этого утверждения на примере. Допустим мы проводим опыты по подбрасыванию симметричной монеты, случайной величиной будем считать объект, принимающий значения 0 выпала решка и 1 выпал орел с вероятностями 0. График распределения вероятности будет иметь следующий вид:.